11 Ajuste linear a partir da IA

Nesta seção nós iremos explorar se ferramentas de inteligência artificial seriam capazes de orientar a análise de regressão e fornecer scripts úteis.

No entanto, cuidado! Recomendamos que todas as saídas fornecidas por IA sejam avaliadas por profissionais competentes na área, que se responsabilizem pelos resultados.

Além disso, dados sensíveis, pessoais ou institucionais, não devem ser fornecidos aos operadores de IA via prompts.

11.1 Atividade Prática 1

Construa um prompt para inteligência artificial com o objetivo de obter orientações estatísticas e um script pronto para a análise de regressão e seleção de modelos.

Prompt

Tarefa: selecionar o modelo que melhor representa a relação entre as variáveis Dose e pH no experimento a seguir;
Contexto: os dados são referentes a um experimento inteiramente aleatorizado com 4 tratamentos e três replicações, cuja finalidade foi observar o efeito da dosagem de essência de limão no pH final de um produto lácteo;
Detalhamento: faça uma comparação estatística entre modelos lineares, determinando qual é o mais parcimonioso; faça diagnóstico do ajuste e análise dos resíduos; verifique, para os modelos ajustados, se há falta de ajuste.
Ferramentas: Linguagem R e funções do stats;
Requisitos: apresente as hipóteses testadas, os testes de significância, os valores p e a interpretação estatística.
Dados: copiar os dados da tabela e colar aqui!

Resposta do chatGPT-4

1. Importar os Dados

Primeiramente, você precisa importar os dados para o R. Você pode criar um data.frame diretamente.

df <- data.frame(
  Unidade = 1:12,
  Tratamentos = rep(LETTERS[1:4], each = 3),
  Dose = rep(c(0, 10, 20, 30), each = 3),
  pH = c(7.3, 6.8, 7.5, 6.5, 6.4, 5.8, 5.2, 4.9, 5.1, 3.2, 2.5, 2.9)
)

1. Ajustar Modelos Lineares

Vamos ajustar alguns modelos lineares e compará-los. Um modelo simples é a regressão linear simples, e outro é um modelo linear com termos polinomiais para considerar efeitos não-lineares da Dose no pH.

# Modelo Linear Simples
modelo_linear <- lm(pH ~ Dose, data = df)

# Modelo Linear Quadrático
modelo_quadratico <- lm(pH ~ poly(Dose, 2), data = df)

1. Comparar Modelos

Vamos comparar os modelos usando o teste de anova.

anova(modelo_linear, modelo_quadratico)

## Analysis of Variance Table
## 
## Model 1: pH ~ Dose
## Model 2: pH ~ poly(Dose, 2)
##   Res.Df     RSS Df Sum of Sq      F   Pr(>F)   
## 1     10 2.08500                                
## 2      9 0.94417  1    1.1408 10.875 0.009264 **
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

1. Diagnóstico do Modelo

Vamos analisar os resíduos dos modelos ajustados.

# Para o Modelo Linear
plot(modelo_linear, 1)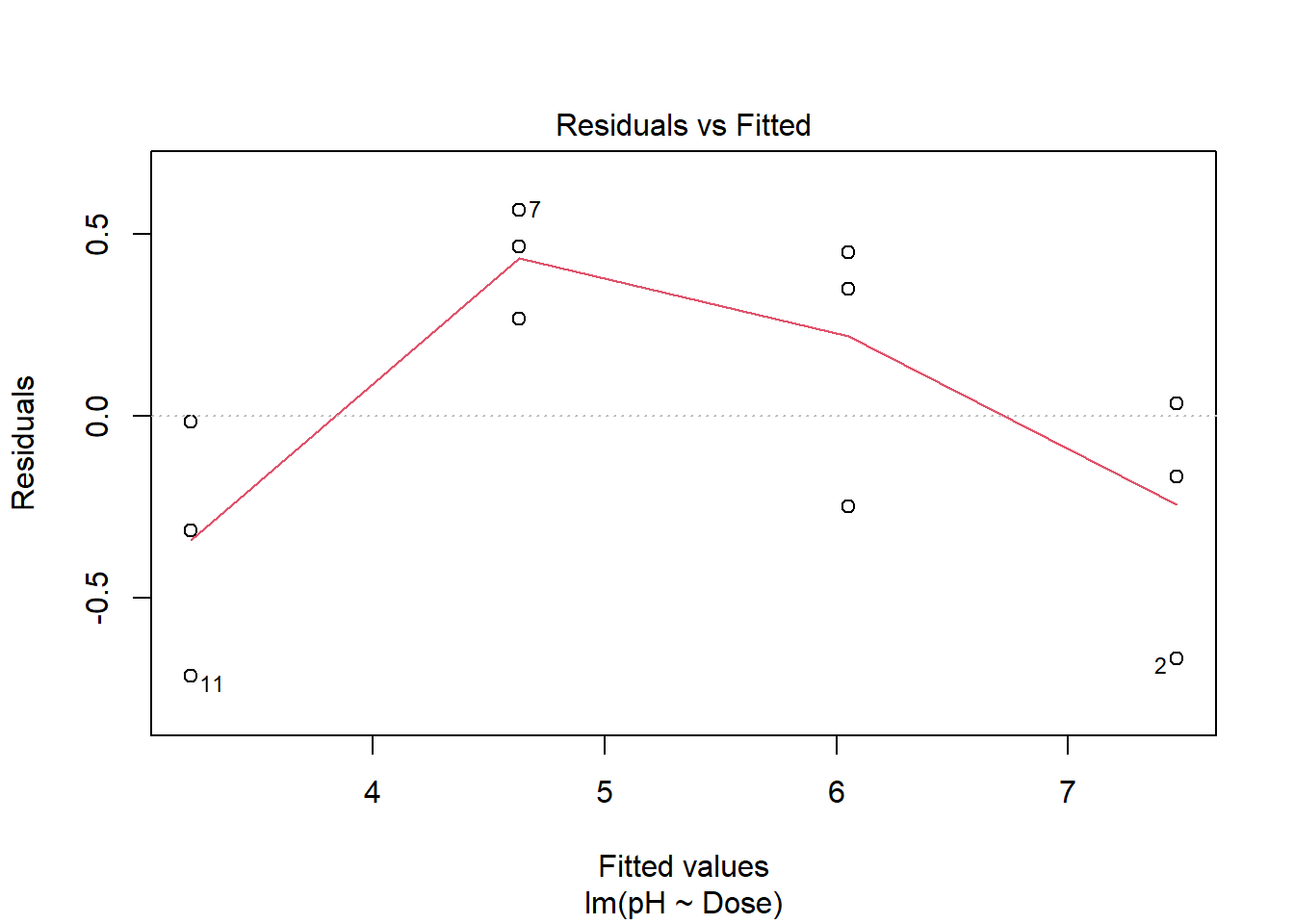

# Para o Modelo Quadrático
plot(modelo_quadratico, 1)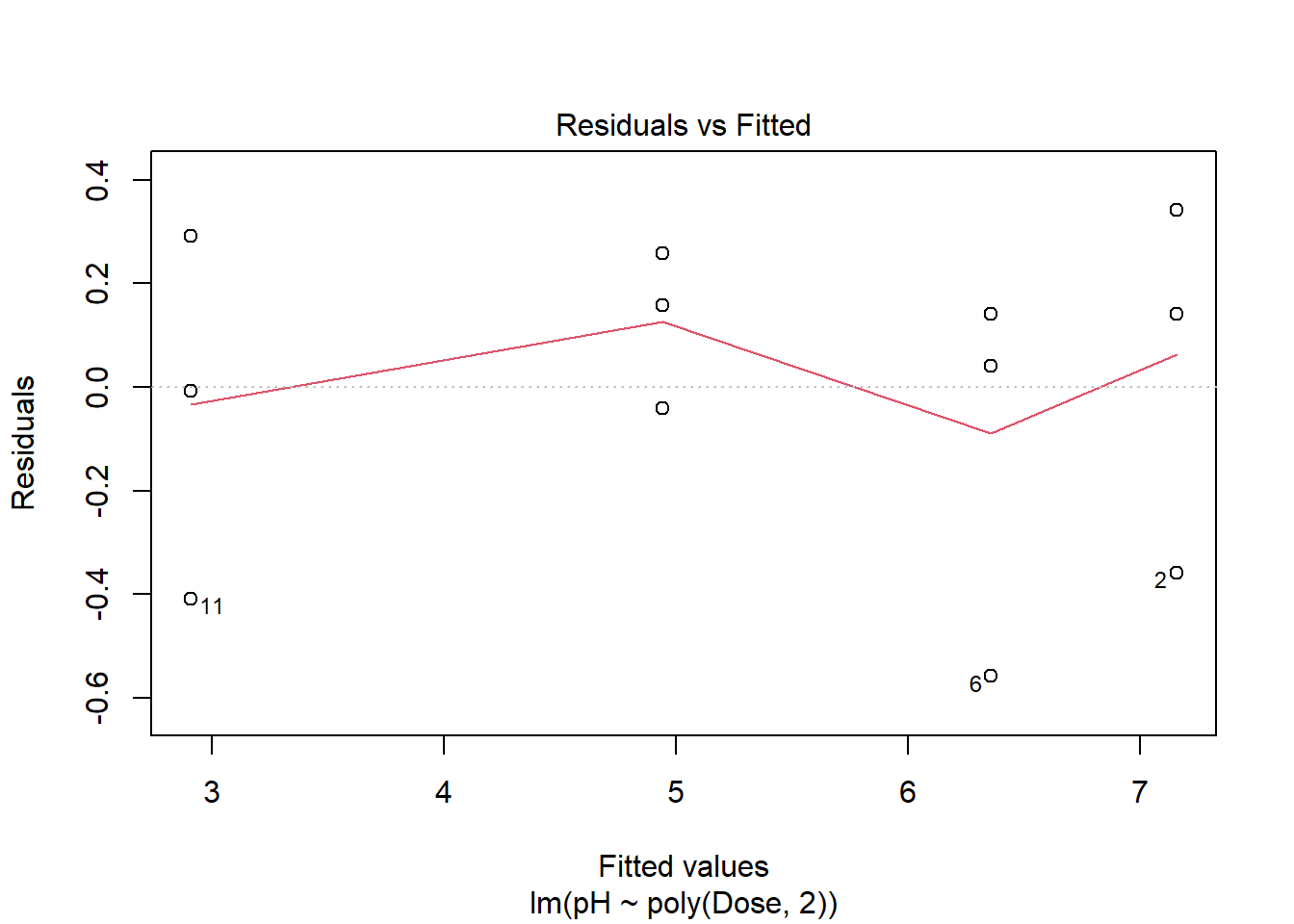

1. Testar a Falta de Ajuste

Para testar a falta de ajuste de cada modelo, podemos comparar a variância dos resíduos de cada modelo.

# Teste de Falta de Ajuste para Modelo Linear
anova(modelo_linear)

## Analysis of Variance Table
## 
## Response: pH
##           Df Sum Sq Mean Sq F value    Pr(>F)    
## Dose       1 30.104 30.1042  144.38 2.885e-07 ***
## Residuals 10  2.085  0.2085                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

# Teste de Falta de Ajuste para Modelo Quadrático
anova(modelo_quadratico)

## Analysis of Variance Table
## 
## Response: pH
##               Df  Sum Sq Mean Sq F value    Pr(>F)    
## poly(Dose, 2)  2 31.2450 15.6225  148.92 1.268e-07 ***
## Residuals      9  0.9442  0.1049                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

1. Interpretação Estatística

Baseado nos p-valores e no diagnóstico dos resíduos, você pode determinar qual modelo é mais apropriado. O modelo com o menor p-valor e os resíduos bem distribuídos (sem padrões aparentes nos gráficos de diagnóstico) será considerado o melhor modelo. Se o p-valor for menor que o nível de significância (geralmente 0,05), você rejeitará a hipótese nula de que não há efeito da Dose no pH.

1. Resumo dos Modelos

Para obter os detalhes dos modelos ajustados, você pode usar a função summary.

# Sumário do Modelo Linear
summary(modelo_linear)

## 
## Call:
## lm(formula = pH ~ Dose, data = df)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.71667 -0.26667  0.00833  0.37500  0.56667 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  7.46667    0.22057   33.85 1.20e-11 ***
## Dose        -0.14167    0.01179  -12.02 2.89e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.4566 on 10 degrees of freedom
## Multiple R-squared:  0.9352, Adjusted R-squared:  0.9287 
## F-statistic: 144.4 on 1 and 10 DF,  p-value: 2.885e-07

# Sumário do Modelo Quadrático
summary(modelo_quadratico)

## 
## Call:
## lm(formula = pH ~ poly(Dose, 2), data = df)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.55833 -0.12083  0.09167  0.18333  0.34167 
## 
## Coefficients:
##                Estimate Std. Error t value Pr(>|t|)    
## (Intercept)      5.3417     0.0935  57.130 7.77e-13 ***
## poly(Dose, 2)1  -5.4867     0.3239 -16.940 3.91e-08 ***
## poly(Dose, 2)2  -1.0681     0.3239  -3.298  0.00926 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.3239 on 9 degrees of freedom
## Multiple R-squared:  0.9707, Adjusted R-squared:  0.9642 
## F-statistic: 148.9 on 2 and 9 DF,  p-value: 1.268e-07

Ao executar esses passos, você terá uma boa ideia de qual modelo melhor representa a relação entre Dose e pH para este conjunto de dados, considerando tanto a significância estatística quanto a adequação do modelo aos dados.

11.2 Atividade Prática 2

Construa um prompt para inteligência artificial com o objetivo de criar uma visualização do ajuste com alta qualidade.

Prompt

Tarefa: visualização do ajuste do modelo quadrático para a variável pH em função da dose;
Contexto: os dados são referentes a um experimento inteiramente aleatorizado com quatro doses e três replicações, cuja finalidade foi observar o efeito da dosagem de essência de limão no pH final de um produto lácteo;
Detalhamento: faça um gráfico do ajuste do modelo quadrático aos dados experimentais seguindo o estado da arte. O gráfico deve apresentar pontos experimentais, reta do ajuste e intervalo com 95% de confiança para os valores preditos da resposta. O gráfico deve ter rótulos adequados para o eixo x e y, além de cores que dêem destaque na visualização.
Ferramentas: Linguagem R e pacote plotly;
Dados: copiar os dados da tabela e colar aqui!

Resposta do chatGPT-4

if(!requireNamespace("dplyr", quietly = TRUE)) install.packages("dplyr")
if(!requireNamespace("plotly", quietly = TRUE)) install.packages("plotly")

library(plotly)
library(dplyr)

# Calculando predições e intervalos de confiança
predicoes <- predict(mod_quad, newdata = dados, interval = "prediction", level = 0.95)

# Adicionando as predições e intervalos de confiança ao data frame
dados <- dados %>%
  mutate(
    fitted = predicoes[,"fit"],
    lwr = predicoes[,"lwr"],
    upr = predicoes[,"upr"]
  )

# Gráfico com plotly
plot_vis <- plot_ly(dados) %>%
  add_trace(
    x = ~Dose, 
    y = ~pH, 
    type = 'scatter', 
    mode = 'markers', 
    name = 'Dados Observados',
    marker = list(color = 'red', size = 10)
  ) %>%
  add_trace(
    x = ~Dose, 
    y = ~fitted, 
    type = 'scatter', 
    mode = 'lines',
    name = 'Ajuste Quadrático',
    line = list(color = 'blue')
  ) %>%
  add_trace(
    x = ~Dose, 
    y = ~lwr, 
    type = 'scatter', 
    mode = 'lines',
    name = 'Limite Inferior 95%',
    line = list(color = 'rgba(173,216,230,0.4)')
  ) %>%
  add_trace(
    x = ~Dose, 
    y = ~upr, 
    type = 'scatter', 
    mode = 'lines',
    name = 'Limite Superior 95%',
    fill = 'tonexty',
    line = list(color = 'rgba(173,216,230,0.4)')
  ) %>%
  layout(
    title = "Ajuste Quadrático do pH em função da Dose",
    xaxis = list(title = "Dose (mg)"),
    yaxis = list(title = "pH")
  )

# Visualizar o gráfico
plot_vis