12 Comparações entre tratamentos

Em experimentos com delineamentos usuais, tais como o inteiramente aleatorizado, as comparações múltiplas podem ser feitas a partir do pacote brasileiro ExpDes.

O ExpDes apresenta uma função para cada tipo de delineamento experimental. Com ele, também é possível realizar a análise de experimentos com tratamentos em esquema fatorial de forma fácil e intuitiva. Porém, o pacote não comporta recursos para delineamentos mais específicos e para a análise de efeitos aleatórios.

Nesta seção, usamos a função crd destinada à análise de Delineamentos Inteiramente Casualizados (Complete Randomized Desing). Nesse comando, a entrata treat designa o vetor de tratamentos, a entrada resp designa o vetor de respostas, quali indica se os tratamentos são qualitativos ou não, e os níveis de significância para os testes T e F são atrivuídos por sigT e sigF, respectivamente.

12.1 Análise quantitativa

# Carregar o pacote expdes
if(!requireNamespace("ExpDes", quietly = TRUE)) install.packages("ExpDes")
library(ExpDes)

# Realizando a análise com a função dic
resultado_dic <- crd(treat = dados$Dose, resp = dados$pH, quali = FALSE, sigT = 0.05, sigF = 0.05)

## ------------------------------------------------------------------------
## Analysis of Variance Table
## ------------------------------------------------------------------------
##            DF     SS     MS     Fc      Pr>Fc
## Treatament  3 31.349 10.450 99.521 1.1293e-06
## Residuals   8  0.840  0.105                  
## Total      11 32.189                         
## ------------------------------------------------------------------------
## CV = 6.07 %
## 
## ------------------------------------------------------------------------
## Shapiro-Wilk normality test
## p-value:  0.1224459 
## According to Shapiro-Wilk normality test at 5% of significance, residuals can be considered normal.
## ------------------------------------------------------------------------
## 
## ------------------------------------------------------------------------
## Homogeneity of variances test
## p-value:  0.7162275 
## According to the test of bartlett at 5% of significance, residuals can be considered homocedastic.
## ------------------------------------------------------------------------
## 
## Adjustment of polynomial models of regression
## ------------------------------------------------------------------------
## 
## Linear Model
## ===========================================
##    Estimate Standard.Error    tc    p.value
## -------------------------------------------
## b0  7.4667      0.1565     47.7028     0   
## b1 -0.1417      0.0084     -16.9324    0   
## -------------------------------------------
## 
## R2 of linear model
## --------
## 0.960286
## --------
## 
## Analysis of Variance of linear model
## ===============================================
##               DF   SS      MS      Fc   p.value
## -----------------------------------------------
## Linear Effect 1  30.1042 30.1042 286.71    0   
## Lack of fit   2  1.2450  0.6225   5.93  0.02634
## Residuals     8  0.8400  0.1050                
## -----------------------------------------------
## ------------------------------------------------------------------------
## 
## Quadratic Model
## ==========================================
##    Estimate Standard.Error   tc    p.value
## ------------------------------------------
## b0  7.1583      0.1824     39.2569    0   
## b1 -0.0492      0.0293     -1.6790 0.1317 
## b2 -0.0031      0.0009     -3.2962 0.0109 
## ------------------------------------------
## 
## R2 of quadratic model
## --------
## 0.996677
## --------
## 
## Analysis of Variance of quadratic model
## ==================================================
##                  DF   SS      MS      Fc   p.value
## --------------------------------------------------
## Linear Effect    1  30.1042 30.1042 286.71    0   
## Quadratic Effect 1  1.1408  1.1408  10.87  0.01092
## Lack of fit      1  0.1042  0.1042   0.99  0.34841
## Residuals        8  0.8400  0.1050                
## --------------------------------------------------
## ------------------------------------------------------------------------
## 
## Cubic Model
## ==========================================
##    Estimate Standard.Error   tc    p.value
## ------------------------------------------
## b0  7.2000      0.1871     38.4856    0   
## b1 -0.1144      0.0718     -1.5943 0.1495 
## b2  0.0032      0.0063     0.4991  0.6311 
## b3 -0.0001      0.0001     -0.9960 0.3484 
## ------------------------------------------
## 
## R2 of cubic model
## -
## 1
## -
## 
## Analysis of Variance of cubic model
## ==================================================
##                  DF   SS      MS      Fc   p.value
## --------------------------------------------------
## Linear Effect    1  30.1042 30.1042 286.71    0   
## Quadratic Effect 1  1.1408  1.1408  10.87  0.01092
## Cubic Effect     1  0.1042  0.1042   0.99  0.34841
## Lack of fit      0     0       0      0       1   
## Residuals        8  0.8400  0.1050                
## --------------------------------------------------
## ------------------------------------------------------------------------

12.2 Análise qualitativa

mpcomp designa o método de comparação múltipla a ser usado

# Realizando a análise com a função dic
resultado_dic <- crd(treat = dados$Dose, resp = dados$pH, quali = TRUE, mcomp = "tukey", sigT = 0.05, sigF = 0.05)

## ------------------------------------------------------------------------
## Analysis of Variance Table
## ------------------------------------------------------------------------
##            DF     SS     MS     Fc      Pr>Fc
## Treatament  3 31.349 10.450 99.521 1.1293e-06
## Residuals   8  0.840  0.105                  
## Total      11 32.189                         
## ------------------------------------------------------------------------
## CV = 6.07 %
## 
## ------------------------------------------------------------------------
## Shapiro-Wilk normality test
## p-value:  0.1224459 
## According to Shapiro-Wilk normality test at 5% of significance, residuals can be considered normal.
## ------------------------------------------------------------------------
## 
## ------------------------------------------------------------------------
## Homogeneity of variances test
## p-value:  0.7162275 
## According to the test of bartlett at 5% of significance, residuals can be considered homocedastic.
## ------------------------------------------------------------------------
## 
## Tukey's test
## ------------------------------------------------------------------------
## Groups Treatments Means
## a     0   7.2 
##  b    10      6.233333 
##   c   20      5.066667 
##    d      30      2.866667 
## ------------------------------------------------------------------------

12.3 Gráfico de médias

12.3.1 Cálculo das margens de erro

Para o cálculo da margem de erro das médias, devemos considerar:

O erro quadrático médio do resíduo (EQMR)

\[ EQMR = \frac{\sum_{i =1}^n (y_i - \hat{y}_i)^2}{df_{res}} \]

O erro padrão da média (SE)

\[ SE = \sqrt{\frac{EQMR}{r}} \]

A margem de erro

\[ erro = t_{(1 - \alpha/2; \, df)} \, \sqrt{\frac{EQMR}{r}} = t_{\alpha/2; \, df} \, SE \]

em que:

\(y_i\) e \(\hat{y}_i\) são os valores observados e preditos da resposta;
\(df_{res}\) é o número de graus de liberdade para os resíduos da análise;
\(r\) é o número de réplicas por tratamentos;
\(t_{(1-\alpha/2; \, df)}\) é o quantil da distribuição \(t\) considerando-se o nível de significância \(\alpha\) e \(df\) graus de liberdade.

(EQMR <- sum( residuals(mod_quali)^2 )/8 )

## [1] 0.105

(SE <- sqrt( EQMR / 3 ))

## [1] 0.1870829

(ERRO <- qt(0.975, 8)*SE)

## [1] 0.4314139

Dessa forma, a margem de erro a se considerar para a estimativa das médias de tratamentos é de \(0,431\) unidades, isso com 95% de confiança.

12.3.2 Prompt para a confecção do gráfico

Prompt

Tarefa: Elabore um gráfico de médias para comparar o pH de um produto sujeito a quatro tratamentos (dosagens)
Contexto: os dados são referentes a um experimento inteiramente aleatorizado com quatro doses e três replicações, cuja finalidade foi observar o efeito da dosagem de essência de limão no pH final de um produto lácteo;
Detalhamento: Faça um gráfico de médias, com barras representando as margens de erro. Use cores diferentes e apresente as letras comparativas do teste. Crie rótulos intuitivos para os eixos. As letras do teste (grupos) devem aparecer acima das colunas que representam cada tratamento.
Ferramentas: Linguagem R e pacote ggplot2 ;
Dados: A margem de erro para as médias é de 0.187. A tabela do teste de Tukey é apresentada a seguir:

Tukey’s Test
Groups	Treatments	Means
a	0	7.2
b	10	6.233333
c	20	5.066667
d	30	2.866667

12.3.3 Resposta do chatGPT-4

Resposta

# Carregar o pacote ggplot2
library(ggplot2)

# Criar o dataframe com os dados do teste de Tukey
dados <- data.frame(
  Tratamento = factor(c('0 ml', '10 ml', '20 ml', '30 ml'), levels = c('0 ml', '10 ml', '20 ml', '30 ml')),
  Médias = c(7.2, 6.233333, 5.066667, 2.866667),
  MargemErro = c(0.187, 0.187, 0.187, 0.187),
  Grupo = c('a', 'b', 'c', 'd')
)

# Criar o gráfico de médias com barras de erro
p <- ggplot(dados, aes(x = Tratamento, y = Médias, fill = Tratamento)) +
  geom_bar(stat = "identity", position = position_dodge(), width = 0.6) +
  geom_errorbar(aes(ymin = Médias - MargemErro, ymax = Médias + MargemErro), 
                width = 0.2, position = position_dodge(0.6)) +
  geom_text(aes(label=Grupo, y=Médias + MargemErro), vjust=-0.5) +
  scale_fill_manual(values = c('0 ml' = 'red', '10 ml' = 'blue', '20 ml' = 'green', '30 ml' = 'purple')) +
  labs(
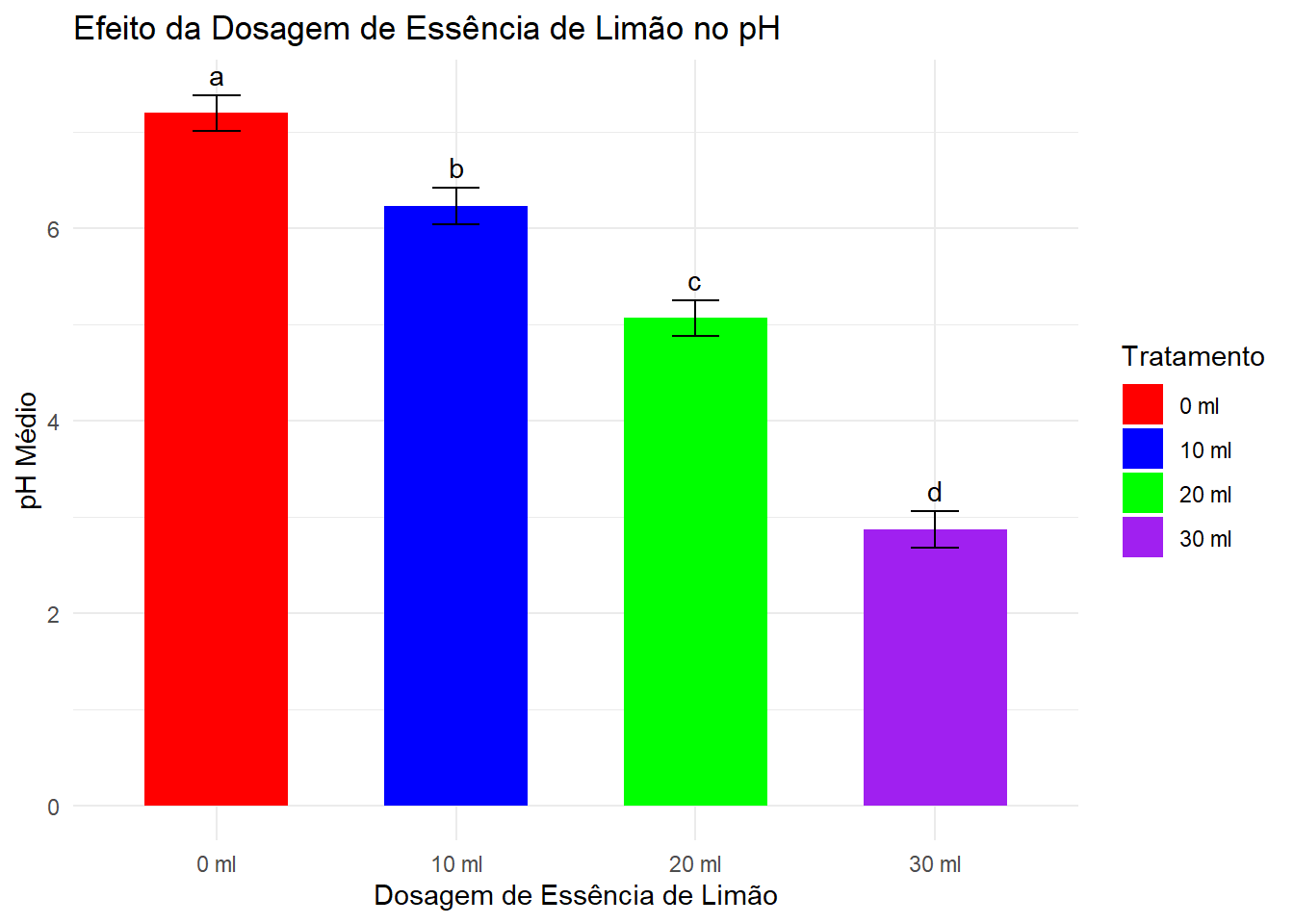
    title = "Efeito da Dosagem de Essência de Limão no pH",
    x = "Dosagem de Essência de Limão",
    y = "pH Médio"
  ) +
  theme_minimal()

print(p)