10 Análise de Regressão

Observe que os tratamentos do experimento podem ser analisados de forma qualitativa ou quantitativa. Na análise quantitativa, por exemplo, desejamos ajustar uma curva de tendência e fazer previsões para novos valores da resposta.

10.1 Ajuste da reta

10.1.1 Ajuste do modelo linear no R

A função lm é usada para ajustar modelos estatisticamente lineares (lm = linear model). Na sintaxe do R, a fórmula pH ~ Dose representa o ajuste de uma reta de tendência, expressa por

\[ pH = \beta_0 + \beta_1 \times Dose \]

mod_reta <- lm( pH ~ Dose, data = dados )
coef( mod_reta )

## (Intercept)        Dose 
##   7.4666667  -0.1416667

Para ajustar a reta de tendência, torna-se necessário calcular os valores mais plausíveis para os parâmetros \(\beta_0\) e \(\beta_1\), com base nos dados. As estimativas de \(\beta_0\) e \(\beta_1\) são obtidas a partir do comando coef.

10.1.2 Diagnóstico do ajuste da reta

Ao realizar o diagnóstico de um ajuste linear clássico a partir dos gráficos dos resíduos, esperamos validar os pressupostos do modelo. Os resíduos devem aparentar ser aleatórios, sem padrões discerníveis, indicando homocedasticidade, e devem ser aproximadamente normalmente distribuídos em torno de zero, validando a suposição de normalidade e a independência dos erros, essencial para inferências subsequentes.

Análise dos resíduos do ajuste

plot( mod_reta, 1) # valores ajustados x resíduos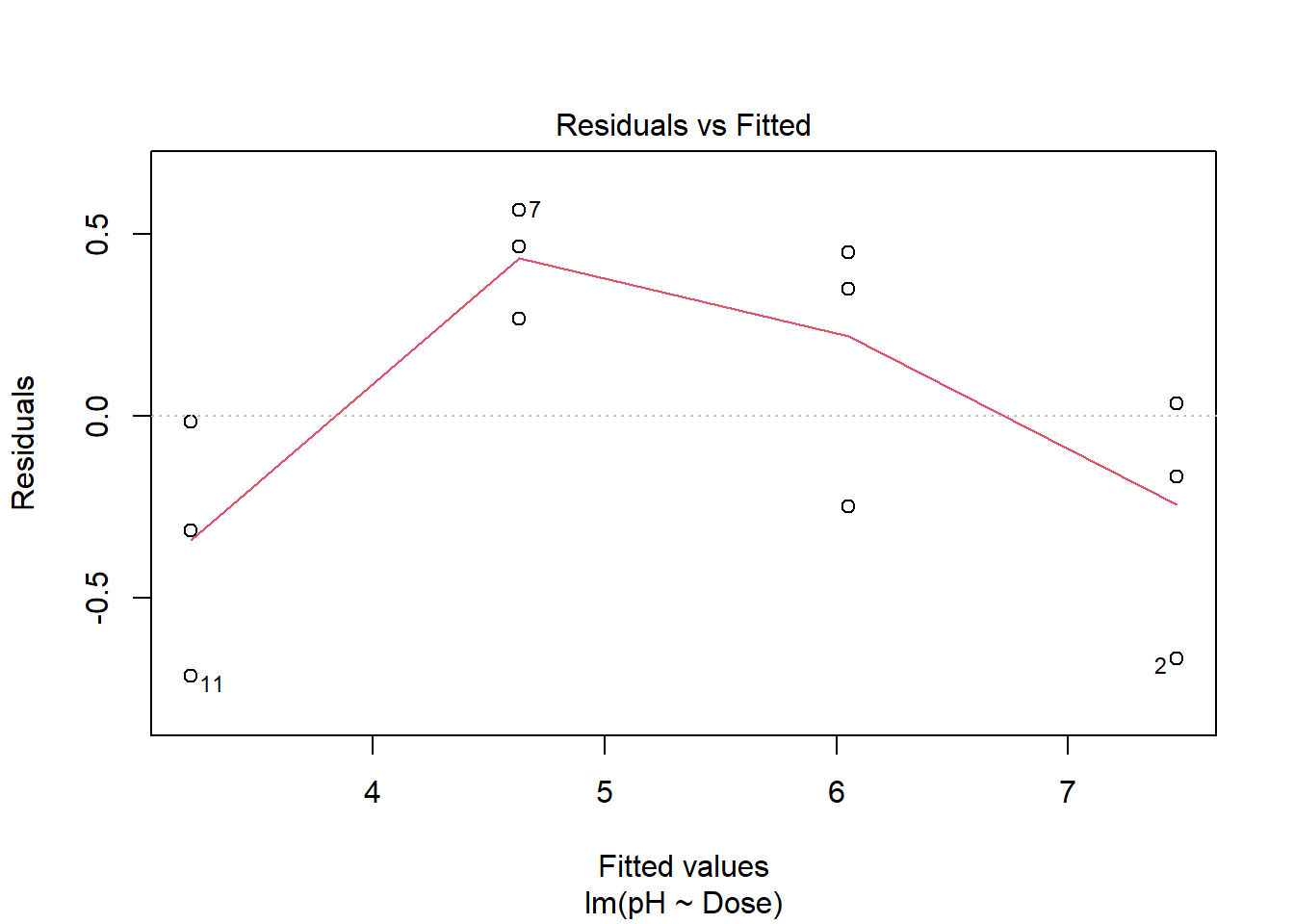

library(car)
qqPlot( residuals( mod_reta ) ) # gráfico quantil-quantil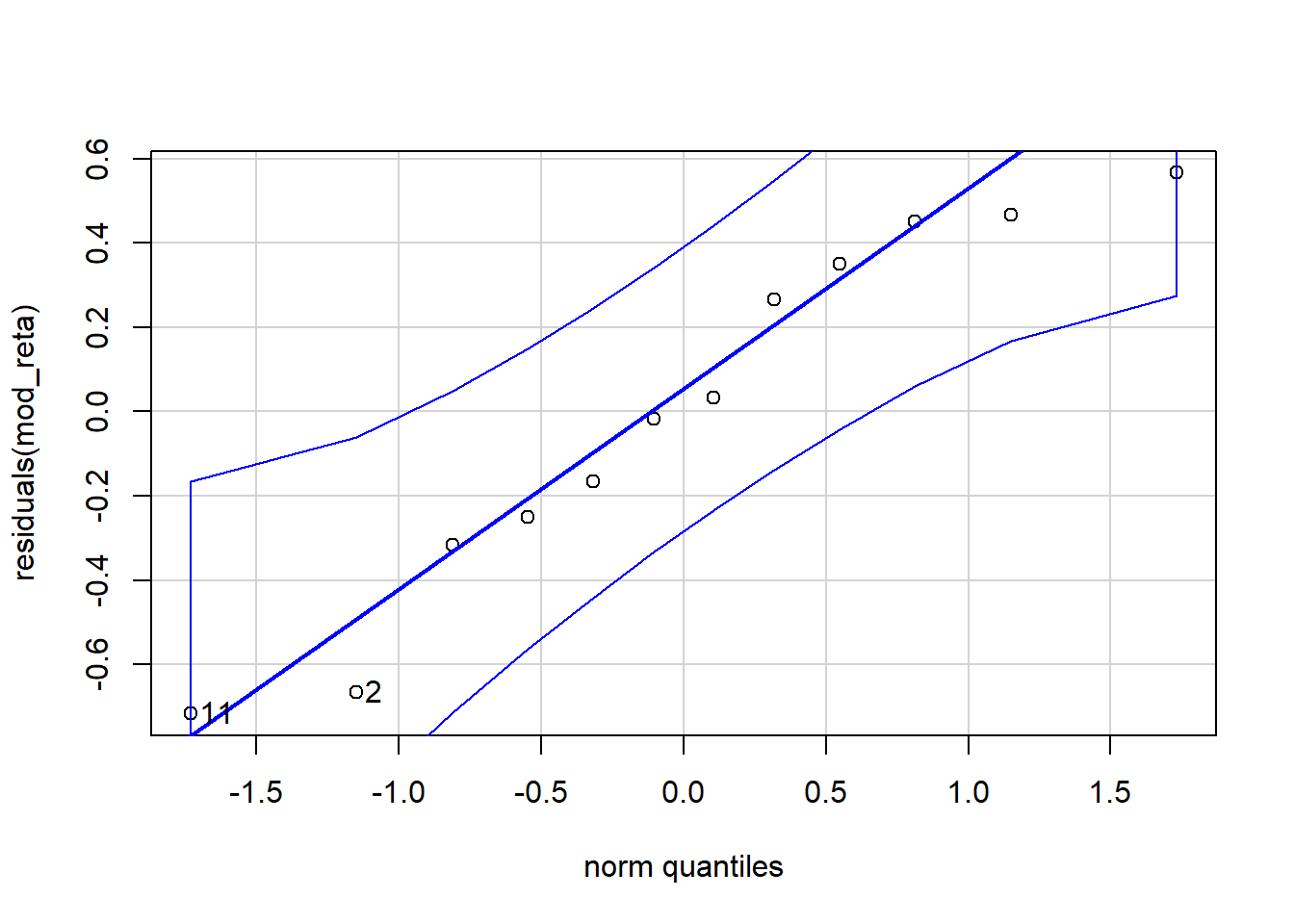

## [1] 11  2

Neste caso, obsevamos que o gráfico quantil-quantil não apresenta desvios à normalidade. Porém, no gráfico dos resíduos em função dos valores ajustados, observa-se uma estrutura de variação dos dados não explicada pelo modelo. Os dados deveriam oscilar aleatoriamente em torno do zero, mas não é isso o que acontece.

10.1.3 Teste de falta de ajuste

Nesta etapa, realizaremos o teste de falta de ajuste para averiguar se o modelo é suficiente para capturar o comportamento dos dados ou se um modelo mais “flexível” deveria ser utilizado.

mod_quali <- lm( pH ~ Tratamentos, data = dados) # ajuste do modelo qualitativo
# Falta de ajuste 
anova( mod_reta, mod_quali )

## Analysis of Variance Table
## 
## Model 1: pH ~ Dose
## Model 2: pH ~ Tratamentos
##   Res.Df   RSS Df Sum of Sq      F  Pr(>F)  
## 1     10 2.085                              
## 2      8 0.840  2     1.245 5.9286 0.02634 *
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Pelo teste F, verifica-se que há falta de ajuste considerando-se o nível de 5% de significância. Conclui-se que o modelo não captura bem o comportamento dos dados

10.1.4 Ajuste do modelo de segundo grau

Com a inserção do termo I(Dose, 2) na fórmula, a expressão da curva de tendência passa a ser

\[ pH = \beta_0 + \beta_1 \times Dose + \beta_2 \times Dose^2 \]

ou seja, uma parábola. Observe que a curvatura exibida por uma parábola pode capturar o comportamento que não foi possível descrever com a reta.

mod_quad <- lm( pH ~ Dose + I(Dose^2), data = dados )
coef( mod_quad )

##  (Intercept)         Dose    I(Dose^2) 
##  7.158333333 -0.049166667 -0.003083333

10.1.5 Diagnóstico do ajuste da parábola

Análise dos resíduos do ajuste

plot( mod_quad, 1) # valores ajustados x resíduos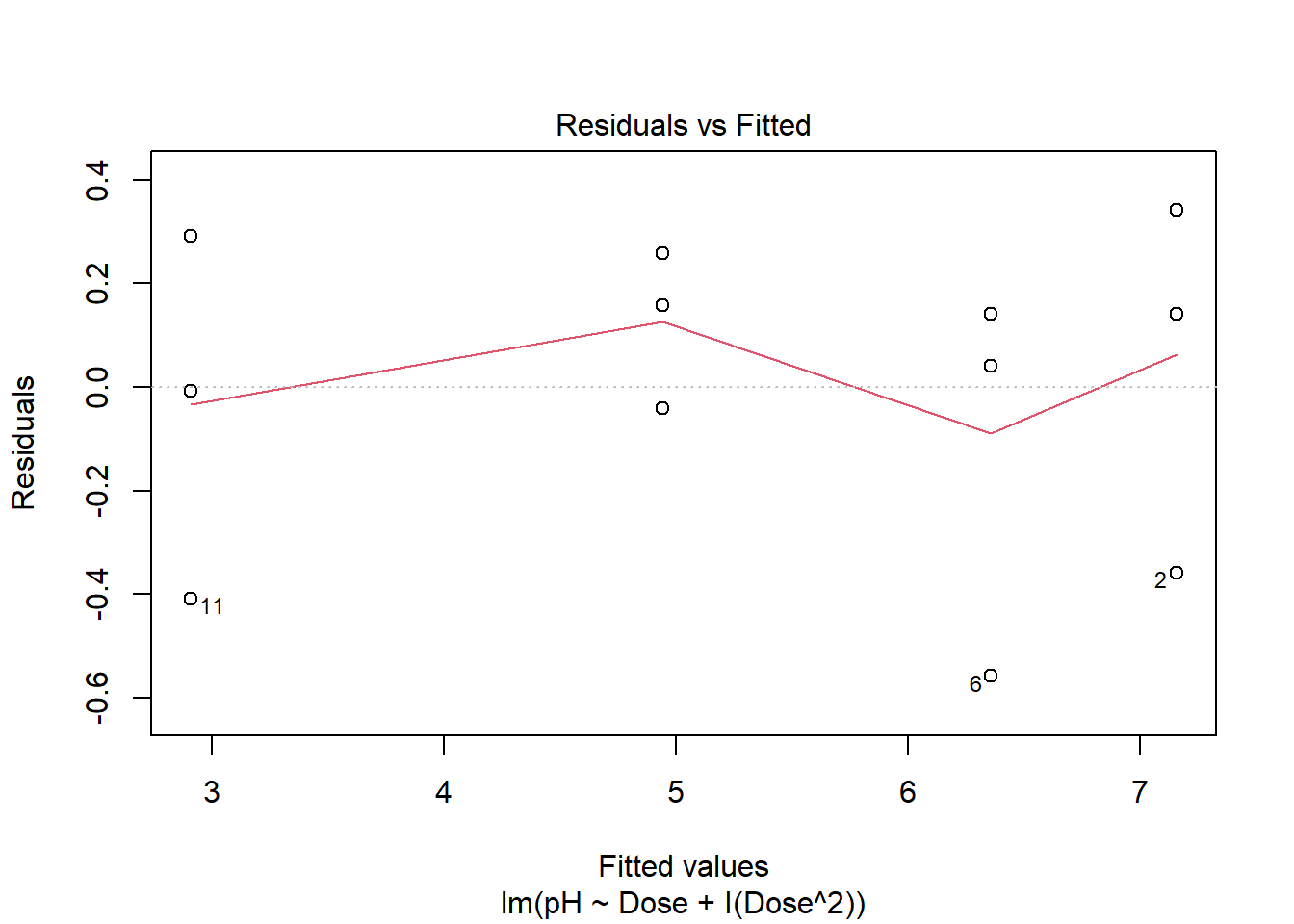

library(car)
qqPlot( residuals( mod_quad ) ) # gráfico quantil-quantil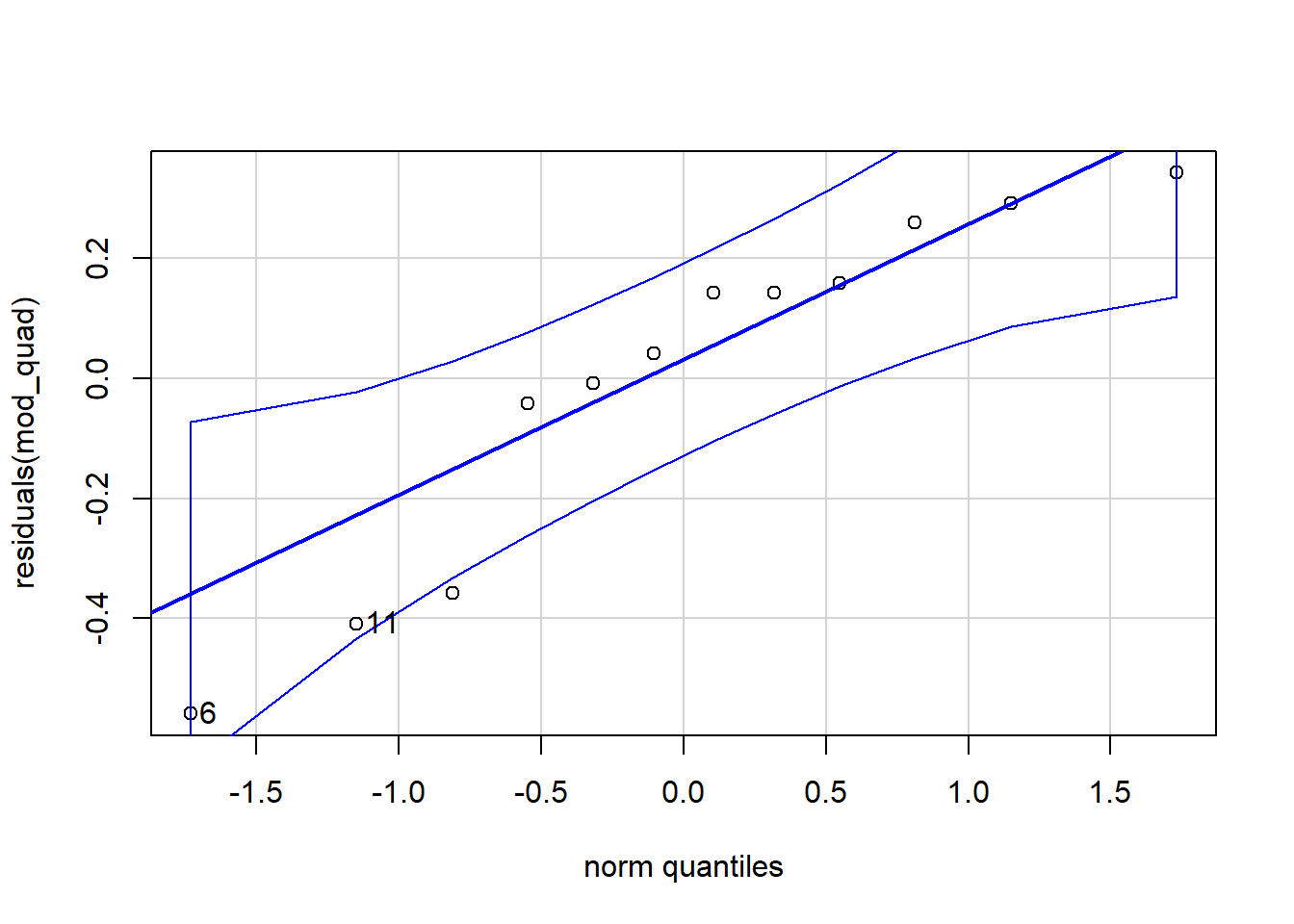

## [1]  6 11

shapiro.test( residuals( mod_quad ) )

## 
##  Shapiro-Wilk normality test
## 
## data:  residuals(mod_quad)
## W = 0.89411, p-value = 0.1332

….

10.1.6 Teste de falta de ajuste para a parábola

# Falta de ajuste 
anova( mod_quad, mod_quali )

## Analysis of Variance Table
## 
## Model 1: pH ~ Dose + I(Dose^2)
## Model 2: pH ~ Tratamentos
##   Res.Df     RSS Df Sum of Sq      F Pr(>F)
## 1      9 0.94417                           
## 2      8 0.84000  1   0.10417 0.9921 0.3484

…

10.1.7 Comparação de modelos

O Critério de Informação de Akaike (AIC) é fundamentado na teoria da informação, proporcionando uma medida relativa da informação perdida quando um determinado modelo é usado para representar o processo gerador dos dados. Ele avalia a adequação do modelo, considerando tanto a complexidade do modelo quanto o ajuste aos dados. O AIC é calculado como \(AIC = 2k - 2\ln(L)\), onde \(k\) é o número de parâmetros no modelo, e \(L\) é a verossimilhança do modelo. Menores valores de AIC indicam um melhor equilíbrio entre ajuste do modelo e complexidade, permitindo comparar modelos diferentes, mesmo não aninhados, proporcionando uma abordagem robusta para a seleção de modelos na análise estatística.

O coeficiente de determinação (R²), por outro lado, apenas mede a proporção da variância explicada pelo modelo, não penalizando a complexidade, podendo levar à preferência por modelos superajustados (overfitting) que performam mal com dados novos. Portanto, o AIC é frequentemente mais adequado para a seleção de modelos quando se compara um conjunto de modelos.

AIC(mod_quali , mod_reta, mod_quad )

##           df      AIC
## mod_quali  5 12.14340
## mod_reta   3 19.05287
## mod_quad   4 11.54621

Neste caso, observa-se que o modelo mais parcimonioso é o quadrático dentre os modelos estudados, pois possui menor perda da informação dos dados originais, além de baixa complexidade, resultando em um AIC inferior.